bio photo

Twitter Github

Writing an Interpretter Using JavaCC

Ever wondered how an interpreter works ? Well, while evaluating parser generators for executing expressions I wrote this small example. Getting to the basics What is an Interpreter ? An interpreter is a computer program that executes the program given to it as an input. In contrast, a compiler generates machine code for the program given to it, which is then executed by the operating system or computer. Lets say the language we are going to interpret supports simple assignment statements like

1 a=1+5;
2 b=a*3;
3 c=a+b;

The execution of this small piece of code would involve four steps

  1. Lexical Analysis
  2. Syntax Analysis
  3. Generation of Abstract Syntax Tree
  4. Execute the code In the lexical analysis phase all the tokens in the code are identified. In out example the tokens are [a, =, 1, +, 5, ; ……]. Once the tokens are identified we need to match them to our defined grammar i.e. many lines of Identifier=Expression;

Defining our language as a Context Free Grammar

The first thing we need to do is to define the grammar of our language as a context free grammar. A context free grammar is a way to define the formal structure in the form

V -> w

Implementing with JavaCC

JavaCC is a parser generator that takes a context free grammar and generates a parser for that language. Lets try to define our grammar in JavaCC. JavaCC would take a .jj file and generate java classes to parse the file and validate the grammar.

Lexical Analysis

We would need to instruct javacc to identify the tokens. The first thing to define in the javacc file is the tokens it needs to skip and the tokens that it needs to scan and parse out.

Now we need to define all the tokens that the parser generated by javacc should parse out

Syntax Analysis

In JavaCC the way to define a production of the form V->e is like

The final grammar defined using the javacc format would look like

language -> (statement)+ # contains one or more statements statement ->
variable=expression; variable -> [“a”-“z”]+ # a variable contains one or more letters from a-z
expression -> additiveExpr
additiveExpr -> multiplyExpr ((+ | -) multiplyExpr)* # can be 5 or (5 + 4) or (5 - 2)
multiplyExpr -> unaryExpr ((* | %) unaryExpr)* # can be 5 or (5 * 4) or (5 % 2)
unaryExpr -> -primaryExpr | primaryExpr # can be 5 or -5
primaryExpr -> number | variable | [1-9]+ # can be  1 or abc

Implementing with JavaCC

JavaCC is a parser generator that takes a context free grammar and generates a parser for that language. Lets try to define our grammar in JavaCC. JavaCC would take a .jj file and generate java classes to parse the file and validate the grammar.

Lexical Analysis

We would need to instruct javacc to identify the tokens. The first thing to define in the javacc file is the tokens it needs to skip and the tokens that it needs to scan and parse out.

SKIP :
{
” “
|“\t“
|“\n“
|“\r“
}

Now we need to define all the tokens that the parser generated by javacc should parse out

TOKEN:
{
<number:>
|       <variable:>
|</variable:></number:>
<divide:>       |     <multiply:>
|</multiply:></divide:>
<plus:>         |       <minus:>
}

Syntax Analysis In JavaCC the way to define a production of the form V->e is like

V() :
{}
{
e()
}

The final grammar defined using the javacc format would look like

 1 PARSER_BEGIN(ExpressionParser)public class ExpressionParser {
 2  
 3 public static void main(String args[]) throws Exception {
 4 ExpressionParser parser = new ExpressionParser(new java.io.FileReader(args[0]));
 5 }
 6 }
 7  
 8 PARSER_END(ExpressionParser)
 9  
10 SKIP :
11 {
12 ” “
13 |“\t“
14 |“\n“
15 |“\r“
16 }
17  
18 TOKEN:
19 {
20 <number:>
21 |       <variable:>
22 |</variable:></number:>
23 <divide:>       |     <multiply:>
24 |</multiply:></divide:>
25 <plus:>         |       <minus:>
26 }</minus:></plus:>ASTstart start() :{}
27 {
28 (statement())+
29 {}
30 }void statement() :
31 {}
32 {
33 identifier()“=”expression()“;”
34 }
35  
36 void identifier() :
37 {}
38 {
39 <variable>
40 {
41 }
42 }</variable>
43  
44 void expression():
45 {}
46 {
47 additiveExpression()
48 }
49  
50 void additiveExpression() :
51 {}
52 {
53 multiplicativeExpression()
54 (
55  
56 <plus> multiplicativeExpression()
57 | <minus> multiplicativeExpression()
58 )*
59 }</minus></plus>void multiplicativeExpression() :
60 {}
61 {
62 unaryExpression()
63 (
64 <multiply> unaryExpression()
65 |</multiply>
66 <divide> unaryExpression()
67 )*
68 }
69 void unaryExpression() :
70 {}
71 {
72 <minus> numberExpression()|
73 numberExpression()
74 }</minus></divide>void numberExpression() :
75 {
76 }
77 {
78 <number>
79 | <variable>
80 }

This would generate ExpressionParser.java which would contain the code requried to parse the defined grammar. On execution of the main method with a file as an argument the parser would pass if there is a valid grammar in the file, or it would throw an exception if the file does not confine to the defined grammar. Now we are done with the lexical and the syntactical analysis. Constructing the Abstract Syntax Tree Now we need to construct the abstract syntax tree. Lets take a simple example

1 a=1+5;
2 b=a*3;
3 c=a+b;

The abstract syntax tree for this should look like 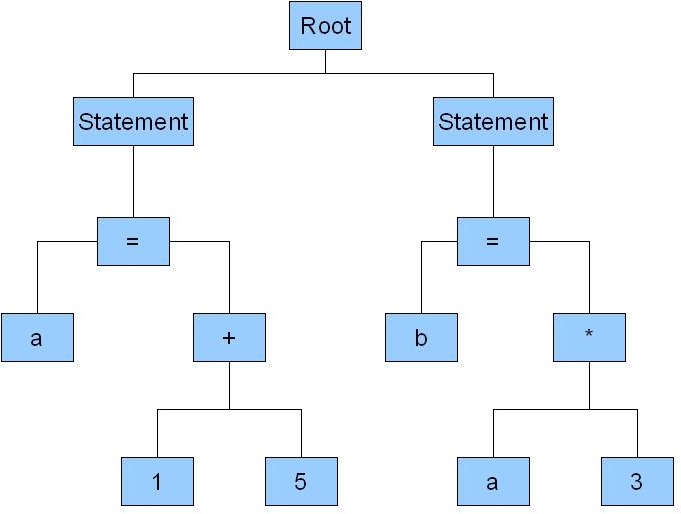AST JavaCC comes along with a preprocessor called jjtree that would create us a abstract syntax tree. Whereever in the grammar we need a tree node we embed # in the grammar definition file.

1 void statement() #Statement:
2 {}
3 {
4 identifier()“=”expression()“;”
5 }

This would create a node ASTStatement.java for the production statement. All nodes by default would extend SimpleNode.java which implements Node that is generated with the node lifecycle methods.

 1 /* Generated By:JJTree: Do not edit this line. Node.java */
 2  
 3 /* All AST nodes must implement this interface.  It provides basic
 4 machinery for constructing the parent and child relationships
 5 between nodes. */
 6  
 7 public interface Node {
 8  
 9 /** This method is called after the node has been made the current
10 node.  It indicates that child nodes can now be added to it. */
11 public void jjtOpen();
12  
13 /** This method is called after all the child nodes have been
14 added. */
15 public void jjtClose();
16  
17 /** This pair of methods are used to inform the node of its
18 parent. */
19 public void jjtSetParent(Node n);
20 public Node jjtGetParent();
21  
22 /** This method tells the node to add its argument to the node’s
23 list of children.  */
24 public void jjtAddChild(Node n, int i);
25  
26 /** This method returns a child node.  The children are numbered
27 from zero, left to right. */
28 public Node jjtGetChild(int i);
29  
30 /** Return the number of children the node has. */
31 public int jjtGetNumChildren();
32  
33 /** Accept the visitor. **/
34 public Object jjtAccept(ExpressionParserVisitor visitor, Object data);
35 }

Our final grammar decorated with all the defintions of the abstract syntax tree nodes would look like

  1 options {
  2 MULTI=true;
  3 VISITOR=true;
  4 NODE_DEFAULT_VOID=true;
  5 NODE_EXTENDS=“BaseNode”;
  6 }
  7  
  8 PARSER_BEGIN(ExpressionParser)
  9  
 10 public class ExpressionParser {
 11  
 12 public static void main(String args[]) throws Exception {
 13 ExpressionParser parser = new ExpressionParser(new java.io.FileReader(args[0]));
 14 //ExpressionParser parser = new ExpressionParser(System.in);
 15 ASTstart expr=parser.start();
 16 ExpressionVisitor v=new ExpressionVisitor();
 17 System.out.println(expr.jjtAccept(v,null));
 18 }
 19 }
 20  
 21 PARSER_END(ExpressionParser)
 22  
 23 SKIP :
 24 {
 25 ” “
 26 |“\t“
 27 |“\n“
 28 |“\r“
 29 }
 30  
 31 TOKEN:
 32 {
 33 <number:>
 34 |       <variable:>
 35 |</variable:></number:>
 36 <divide:>       |     <multiply:>
 37 |</multiply:></divide:>
 38 <plus:>         |       <minus:>
 39 }</minus:></plus:>ASTstart start() #start:{}
 40 {
 41 (statement())+
 42 { return jjtThis; }
 43 }void statement() #Statement:
 44 {}
 45 {
 46 identifier()“=”expression()“;”
 47 }
 48  
 49 void identifier() :
 50 {}
 51 {
 52 <variable>
 53 {
 54 jjtThis.data.put(“name”,token.image);
 55 }#Variable
 56 }</variable>
 57  
 58 void expression():
 59 {}
 60 {
 61 additiveExpression()
 62 }
 63  
 64 void additiveExpression() :
 65 {}
 66 {
 67 multiplicativeExpression()
 68 (
 69  
 70 <plus> multiplicativeExpression()#AddExpr(2)
 71 | <minus> multiplicativeExpression()#SubractExpr(2)
 72 )*
 73 }</minus></plus>void multiplicativeExpression() :
 74 {}
 75 {
 76 unaryExpression()
 77 (
 78 <multiply> unaryExpression()#MultiplyExpr(2)
 79 |</multiply>
 80 <divide> unaryExpression()#DivideExpr(2)
 81 )*
 82 }
 83 void unaryExpression() :
 84 {}
 85 {
 86 <minus> numberExpression()#NegateExpr(1)|
 87 numberExpression()
 88 }</minus></divide>void numberExpression() :
 89 {
 90 }
 91 {
 92 <number>
 93 {
 94 jjtThis.data.put(“value”,new Integer(Integer.parseInt(token.image)));
 95 }#Number
 96 | <variable>
 97 {
 98 jjtThis.data.put(“name”,token.image);
 99 }#VariableValue
100 }

If you notice in the option, we have instructed jjtree to extend all sources from BaseNode.java. The base node is decorated with a hashmap that would be used to store the scanned tokens during parsing.

1 import java.util.HashMap;</variable></number>public class BaseNode{
2 public HashMap data=new HashMap();
3 }

If you observe line 99 of the grammar definition, it shows how the parsed number token is added to the Number node that is constructed by jjtree. This completes the generation of the abstract syntax tree. Interpretation and Execution What now remaing is to walk the tree and execute the code. One of the options that we have specified in the grammar definition is to generate the visitor. JJtree would automatically add accept methods on all the nodes generated and also generate the visitor interface

 1 void statement() #Statement:
 2 /* Generated By:JJTree: Do not edit this line. C:\workspace\JavaCC\target\ExpressionParserVisitor.java */
 3  
 4 public interface ExpressionParserVisitor
 5 {
 6 public Object visit(SimpleNode node, Object data);
 7 public Object visit(ASTstart node, Object data);
 8 public Object visit(ASTStatement node, Object data);
 9 public Object visit(ASTVariable node, Object data);
10 public Object visit(ASTAddExpr node, Object data);
11 public Object visit(ASTSubractExpr node, Object data);
12 public Object visit(ASTMultiplyExpr node, Object data);
13 public Object visit(ASTDivideExpr node, Object data);
14 public Object visit(ASTNegateExpr node, Object data);
15 public Object visit(ASTNumber node, Object data);
16 public Object visit(ASTVariableValue node, Object data);
17 }

All we need to do now is to implement the visitor interface and interpret our language. The Interpreter would need two datastores

  1. Symbol Table
  2. Execution Stack The symbol table would hold all the variables and their values, and the execution stack would contain all the intermediate results while expression are evaluated. The Visitor code would look like.
 1 public interface ExpressionParserVisitor
 2  
 3 import java.util.HashMap;
 4 import java.util.LinkedList;
 5  
 6 public class ExpressionVisitor implements ExpressionParserVisitor{
 7  
 8 private LinkedList stack=new LinkedList();
 9 private HashMap symbolTable=new HashMap();
10  
11 public Object visit(SimpleNode node, Object data) {
12 node.childrenAccept(this,data);
13 return null;
14 }
15  
16 public Object visit(ASTstart node, Object data) {
17 node.childrenAccept(this,data);
18 return symbolTable;
19 }
20  
21 public Object visit(ASTAddExpr node, Object data) {
22 node.childrenAccept(this,data);
23 Integer arg1=pop();
24 Integer arg2=pop();
25 stack.addFirst(new Integer(arg2.intValue()+arg1.intValue()));
26 return null;
27 }
28  
29 public Object visit(ASTSubractExpr node, Object data) {
30 node.childrenAccept(this,data);
31 Integer arg1=pop();
32 Integer arg2=pop();
33 stack.addFirst(new Integer(arg2.intValue()-arg1.intValue()));
34 return null;
35 }
36  
37 public Object visit(ASTMultiplyExpr node, Object data) {
38 node.childrenAccept(this,data);
39 Integer arg1=pop();
40 Integer arg2=pop();
41 stack.addFirst(new Integer(arg2.intValue()*arg1.intValue()));
42 return null;
43 }
44  
45 public Object visit(ASTDivideExpr node, Object data) {
46 node.childrenAccept(this,data);
47 Integer arg1=pop();
48 Integer arg2=pop();
49 stack.addFirst(new Integer(arg2.intValue()/arg1.intValue()));
50 return null;
51 }
52  
53 public Object visit(ASTNegateExpr node, Object data) {
54 node.childrenAccept(this,data);
55 Integer arg1=pop();
56 stack.addFirst(new Integer(arg1.intValue()*-1));
57 return null;
58 }
59  
60 public Object visit(ASTNumber node, Object data) {
61 node.childrenAccept(this,data);
62 stack.addFirst(node.data.get(“value”));
63 return null;
64 }
65  
66 public Object visit(ASTStatement node, Object data) {
67 node.childrenAccept(this,data);
68 Integer value=(Integer)stack.removeFirst();
69 String var=(String)stack.removeFirst();
70 symbolTable.put(var,value);
71 return null;
72 }
73  
74 public Object visit(ASTVariable node, Object data) {
75 node.childrenAccept(this,data);
76 String var=(String)node.data.get(“name”);
77 stack.addFirst(var);
78 return null;
79 }
80  
81 public Object visit(ASTVariableValue node, Object data) {
82 node.childrenAccept(this,data);
83 String var=(String)node.data.get(“name”);
84 stack.addFirst(symbolTable.get(var));
85 return null;
86 }
87  
88 private Integer pop()
89 {
90 return (Integer)stack.removeFirst();
91 }
92  
93 }

Well, thats it .. our very own interpretter !! Fork at Github

bio photo

Twitter Github

Writing an Interpretter Using JavaCC was published on .